星を SVG で描画したい

Small Sketch という Android アプリのアイコンで星型を使いたくなったので、星をSVGで記述する必要が生じた. 星は円周上の5つの点を直線で結ぶとできる図形. 円周上の点の計算といえば三角関数、それから直線の交点の計算、それらの点を結ぶと星のパスが描画できる. これらの計算処理をまとめます.

star.svg

完成した star.svg はこちら.

<svg xmlns="http://www.w3.org/2000/svg" width="320" height="320" viewBox="0 0 24 24">
    <path stroke="none" fill="rgb(199,133,80)" d="M23.999999817229558 12.002094395044947 L15.707734134995487 14.694815305652586 L15.706211562383146 23.413325363576448 L10.582831059890982 16.35900868825696 L2.2905658368936734 19.05172944973811 L7.416408293225771 11.999201933101395 L2.293026593511586 4.944883609342316 L10.584354192146694 7.640498790409893 L15.710197709212746 0.5879698143339773 L15.708675136549694 9.30648016263852 L23.999999817229558 12.002094395044947 z" />
</svg>

cairosvg

とりあえず、SVGをPNGに変換できるように

sudo apt install python-cairosvg

などとして cairosvg コマンドを入れておきましょう.

cairosvg star.svg -o star.png

とすれば star.png が出力できます.

基本方針

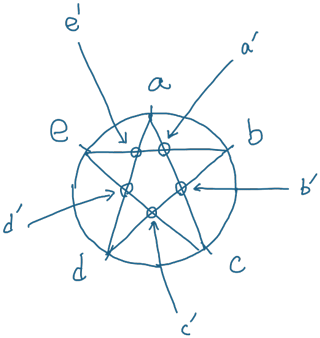
星を描くために まず円周を5等分した円周上の点 a,b,c,d,e を考えます. 次に線分 ac と be の交点を a' , 線分 ac と bd の交点を b' , ・・・のようにして 点 a', b', c', d', e' を計算. これら a a' b b' c c' d d' e e' a をつなげたパスが星になります.

fivepoints.kts : 円周上の5つの点の計算

原点を中心に半径 r の円を考えます. 円周を5等分するので、それらの点と原点を結んだ線分同士がつくる角度は 72, 144, 216...度になります. 三角関数をつかえば 原点を中心にした半径 r の円の円周上の点は ( cosθ * r, sinθ * r ) になるので以下のようなスクリプトで計算できます.

角度から cosθ を求めるには Math.cos( radian ) を使います. このメソッドを使うには角度からradian を求める必要がありますが、Math.toRadians(角度) を使えばOKです.

import java.awt.geom.Point2D

class FivePointCalculator(val r: Int){
    fun points(): List<Point2D>{
        return 0.until(360).step(72).map { degree->
            val radian = Math.toRadians( degree.toDouble() )
            val x = Math.cos(radian)*r 
            val y = Math.sin(radian)*r 
            Point2D.Double(x,y)
        }
    }
}

val points = FivePointCalculator(12).points()
System.out.println(points)

crosspoint.kts : 直線の交点の計算

直線の交点座標を計算するためのコードを書きます.

import java.awt.Point

data class Line(val startPt: Point, val stopPt: Point)

class CrossPointCalculator(val line0: Line, val line1: Line) {
    fun crossPoint(): Point{
        val x1 = line0.startPt.x
        val y1 = line0.startPt.y
        val x2 = line0.stopPt.x
        val y2 = line0.stopPt.y

        val x3 = line1.startPt.x
        val y3 = line1.startPt.y
        val x4 = line1.stopPt.x
        val y4 = line1.stopPt.y

        val a1 = (y2-y1)/(x2-x1)
        val a3 = (y4-y3)/(x4-x3)

        val x = (a1*x1 - y1- a3*x3 +y3)/(a1-a3)
        val y = (y2-y1)/(x2-x1)*(x-x1)+y1

        return Point(x,y)
    }
}

val line0 = Line(Point(-10,-10), Point(10, 10))
val line1 = Line(Point(-10, 10), Point(10,-10))
val crossPt = CrossPointCalculator(line0, line1).crossPoint()
System.out.println(crossPt)

kotlin script なので、 kotlinc -script crosspoint.kts として実行すると 結果の点 (0,0) が出力されます. これを使えば a' 〜 e' の座標を計算できます.

star.kts : 星を描画するためのすべての点を計算

fivepoints.kts と crosspoint.kts を使って星を描画するためのすべての点を計算するスクリプトを書きます. なお fivepoints.kts は そのままでは 原点を中心として座標計算した結果、マイナスの値になる点があり不都合なので、 半径の値分だけ x と y 座標値を平行移動することで、すべての点の座標値を 0 以上の値にしておきます.

また、直線の交点を求めるメソッドが（ いい加減な実装のため ）特定の値の場合、意図通り計算できないため（ バグじゃん ） そのような値を避けるように FivePointCalculator クラス側で、radian 計算部分で 角度 + 0.01f しています.

import java.awt.Point
import java.awt.geom.Point2D

class FivePointCalculator(val r: Int){
    fun points(): List<Point2D>{
        return 0.until(360).step(72).map { degree->
            val radian = Math.toRadians( (degree+0.01f).toDouble() )
            val x = Math.cos(radian)*r 
            val y = Math.sin(radian)*r 
            Point2D.Double(x +r, y +r) // 平行移動
        }
    }
}

data class Line(val startPt: Point2D, val stopPt: Point2D)

class CrossPointCalculator(val line0: Line, val line1: Line) {
    fun crossPoint(): Point2D.Double {
        val x1 = line0.startPt.x
        val y1 = line0.startPt.y
        val x2 = line0.stopPt.x
        val y2 = line0.stopPt.y
    
        val x3 = line1.startPt.x
        val y3 = line1.startPt.y
        val x4 = line1.stopPt.x
        val y4 = line1.stopPt.y
    
        val a1 = (y2-y1)/(x2-x1)
        val a3 = (y4-y3)/(x4-x3)

        val x = (a1*x1 - y1- a3*x3 +y3)/(a1-a3)
        val y = (y2-y1)/(x2-x1)*(x-x1) +y1
    
        return Point2D.Double(x,y)
    }
}

var r = 12
val points = FivePointCalculator(r).points()

val a = points[0]
val b = points[1]
val c = points[2]
val d = points[3]
val e = points[4]

val aDash = CrossPointCalculator( Line(a,c), Line(b,e) ).crossPoint()
val bDash = CrossPointCalculator( Line(b,d), Line(a,c) ).crossPoint()
val cDash = CrossPointCalculator( Line(c,e), Line(b,d) ).crossPoint()
val dDash = CrossPointCalculator( Line(d,a), Line(e,c) ).crossPoint()
val eDash = CrossPointCalculator( Line(e,b), Line(a,d) ).crossPoint()

val svgCmdList = mutableListOf<String>()
svgCmdList.add("M${a.x} ${a.y}")
svgCmdList.add("L${aDash.x} ${aDash.y}")
svgCmdList.add("L${b.x} ${b.y}")
svgCmdList.add("L${bDash.x} ${bDash.y}")
svgCmdList.add("L${c.x} ${c.y}")
svgCmdList.add("L${cDash.x} ${cDash.y}")
svgCmdList.add("L${d.x} ${d.y}")
svgCmdList.add("L${dDash.x} ${dDash.y}")
svgCmdList.add("L${e.x} ${e.y}")
svgCmdList.add("L${eDash.x} ${eDash.y}")
svgCmdList.add("L${a.x} ${a.y}")
svgCmdList.add("z")

val svgCmd = svgCmdList.joinToString( separator = " " )

System.out.println("""<svg xmlns="http://www.w3.org/2000/svg" width="320" height="320" viewBox="0 0 24 24">
    <path stroke="none" fill="rgb(199,133,80)" d="${svgCmd}" />
</svg>""")

星のとんがりが真上にこないのが気に入らない場合は val radian = Math.toRadians( (degree+0.01f).toDouble() ) を val radian = Math.toRadians( (90+degree+0.01f).toDouble() ) として 90 度足すことで修正できます.